[0001D] Maya MEL Photo Converter to a Single Polyline

I’ve begun the process of developing custom plug-ins and scripts to export 2D CNC designs.  Loosely based on the growth of moss, the first experiment is being able to draw a picture using just one single polyline, since I don’t have Z-axis capability yet.  With Z-axis capability, I can lift the pen off of the paper, but as the Monster currently stands, it can just do X and Y.  I’ll have more information about the progress with running this on the Monster here.

Task:  To make an image using just one Polyline.

I tried a couple different techniques, but ended up using a pseudo-randomized and pseudo-recursive system.  Moss grows recursively, and this is a single line, so I’m already diverging from the aesthetic a little.  The script weighs the RGB values from a pre-applied jpg in Maya and makes a matrix of brightness values.  Unfortunately, Maya MEL doesn’t handle nested arrays well (matrices), so I had to do a string array hack.  Ideally, I’d love to rewrite this in C#, but at the moment, I’m just too excited to invest in that since I just wanted to make a cool thing to test the Monster.

Once the matrix is filled, the script takes the lowest numbers and begins a path through the darkest numbers.  In Maya MEL, the color brightness is inverted (0.0 = black and 1.0 = white).  Once the darkest numbers are taken in a particular region, the subroutine returns a zero vector, and the recursion allows for it to find a nearby dark region to propagate.  Once all the major regions are taken, it has one more level of recursion to find something.

I should really revise this to be actually-recursive, but since I was just jamming it out, it’s going to stay at 3 levels.

I posted the GetRGBGrid on the 0001d wiki.  Here is the code:

global proc string[] GetRGBGrid(string $FileName, int $xMax, int $yMax ) {
//0001D LLC 2015 Nick Pisca
//int $xMax = 5; int $yMax = 6; string $FileName = "file1";
//eval("matrix $Acc["+$xMax+"]["+$yMax+"]");
string $wstr[] ; 

for ($x=0;$x<=$xMax;$x++) {
float $xf = float($x)/float($xMax);
print ("Collecting RGB's " + $x + " of " + $xMax + ".\n");
string $wsub = "";
for ($y=0;$y<=$yMax;$y++) { 			float $yf = float($y)/float($yMax);

//select -r ("nurbsPlane1.uv["+($xf)+"]["+($yf)+"]");

float $rdb[] = `colorAtPoint -u $xf -v $yf $FileName`;

if (($rdb[0] > 0.5) && ($rdb[0] < 0.9)) { 				float $RRand = rand(0.0,0.999);

if ($RRand > 0.90) {
float $FRand = $rdb[0]/2.0; //rand(0.5,0.999);
$wsub = $wsub + $FRand + ",";
} else {
$wsub = $wsub + $rdb[0] + ",";
}
} else {
$wsub = $wsub + $rdb[0] + ",";
}
//$Acc[$x][$y] = $rdb[0];
}
$wstr[$x] = $wsub;
}

 return $wstr;
}

You are probably wondering why there is some randomness in there.  Ideally, that shouldn’t be there.  If you are planning on using this subroutine, I advise you to get rid of it.  However, I was working with an image with too much white, and I wanted a small likelihood that the code could migrate off course a little.  This gives the script a better chance to grow into new patches of color.

I created a bunch of emergent subroutines that use vector math to retrieve nearest neighbor RGB’s.

GetDarkestVector reads all the RGB’s and returns the darkest spot in the whole image.

GetDarkestIndices finds the U and V grid coordinates from the string array hack.  Good to have to simplify things.

FindDarkestNeighbor is a curious function, because it allows the user to search the whole image, its nearest neighbor, and any dark patch within a gridded radius.

The beauty of the matrix allows me to store the RGB values without querying the image, which is a little slow.  However, I might remove this functionality so that further enhancements of the script allow for better emergent path propagation.

After tweaking the inputs, I finally got a polyline that resembled the image but also didn’t take 6 hours to run.  This path is about 6″ tall and 4″ wide.  As stated in the aforementioned Sherpa post, it took about 20 minutes to run on the CNC monster.

Here’s an overlay of the image (transparent) and the single polyline path (in dark blue):

Hiding the image shows just the polyline path.

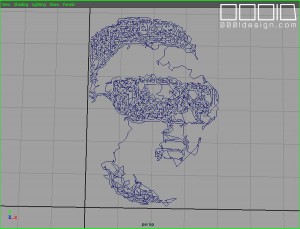Cool.  That’ll be a nice first test sample.

Onward!