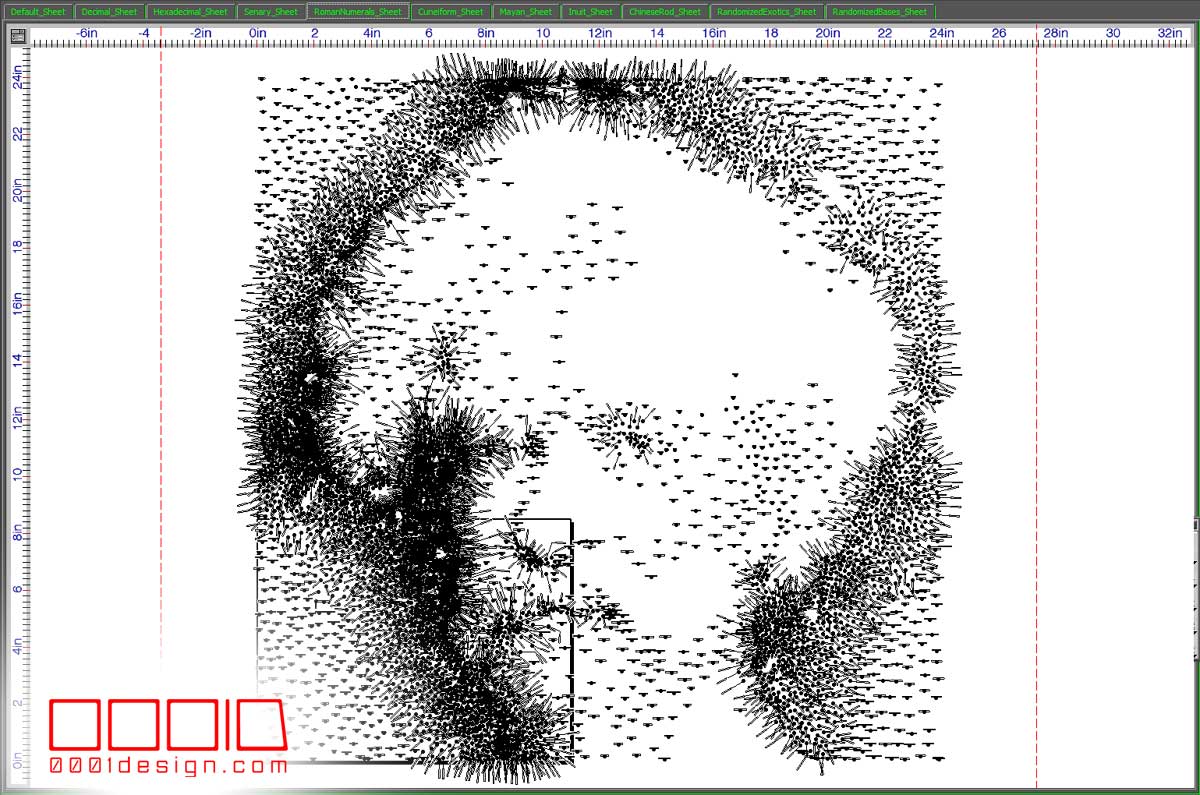
Some of the Mega-Dots Puzzles have small numbers and some have some massive numbers. In order to make the large numeral puzzles legible, I developed ways to optimize the orientation of the tags and leaders in CATIA.
The small number puzzles were pretty simple to code. By tagging a dot in 2D, the string is placed center justified above the point. The only tricky part was ensuring there was a small gap between the top of the dot and bottom of the text. This was resolved by selecting the text only objects and moving them manually in the CATDrawing. The following number systems fell in to the category of “small numbers.”
- Decimal Numbers
- Alphanumeric
- Babylonian
- Inuit
- Mayan
Since the older number sets use a larger base, they require fewer numerals to express a larger number. For example, in Babylonian numerals, the characters:
and
The larger the number gets, the more efficient the Babylonian numerals gets. This is kind of cruddy for the average person trying to use Babylonian numbers for everyday things, like accounting, pricing, and basic counting, but it’s wonderful for a connect-the-dots game, or any numbering situation that has limited space.
Converse to that, there exists the “large number” Mega-Dots puzzles. These puzzles have numbers that are exceedingly long, either due to their small bases, or due to their convoluted numeral structure. Examples of these are:
- Roman Numerals
- Randomized Bases
- Binary System
Early in the development of the puzzle, it became apparent that the standard tag distribution that comes in CATIA by default would not suffice. There were portions of the puzzle that had sometimes as many as a dozen overlapping tags at once. Not even making a manual process of adjusting the tags would work, or even if it would, it would require days of tweaking. I’m not a fan of excessive post-processing.
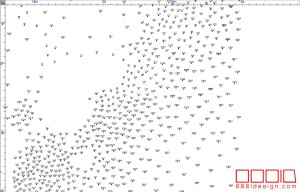
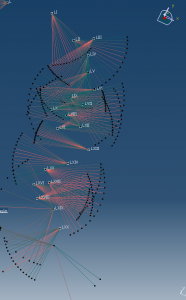
The image to the right shows how I accomplished the tag and leader optimization. It’s actually a basic concept. Just make an array of rotating lines emanating from the point, and calculate the optimal location that is furthest from its neighbors. The greenest lines are the most optimal locations.
Then, while processing this array of angles, using a recursive process, include the locations of the tag and potential leader. This excludes the new leaders as the old leaders are recursively limiting the available space. In order to accomplish this, I used a variety of ported vector math subroutines 1 2 3 4 (I didn’t want to lead the .net libraries for vectors, so I just made my own vector subs), and developed a 2D line measuring function, located on our wiki. This function allows me to ensure that my whole leader line is detected and not just the dots and tags.
static double[] Get2DClosestPointToLineSegment(double[] A, double[] B, double[] OffPt, bool SkipExtremities)
{
double mAB = (B[1] - A[1]) / (B[0] - A[0]);
double mCD = -1 * (B[0] - A[0]) / (B[1] - A[1]);
double bAB = B[1] - (mAB * B[0]);
double bCD = OffPt[1] - (mCD * OffPt[0]);
double fx = (bCD - bAB) / (mAB - mCD);
double fy = (mAB * fx) + bAB;
double[] D = {fx, fy, 0.0};
double[] diff = ArraySubtraction(D, OffPt);
double DistMag = ArrayVectorMag(diff);
double[] diffAB = ArraySubtraction(A, B);
double[] diffAD = ArraySubtraction(D, A);
double[] diffBD = ArraySubtraction(D, B);
double magAB = ArrayVectorMag(diffAB);
double magAD = ArrayVectorMag(diffAD);
double magBD = ArrayVectorMag(diffBD);
double[] winA = {0.0,0.0,0.0,0.0};
if (magAB < (magAD + magBD - 0.00001))
{
if (SkipExtremities == true)
{
winA[0] = 10000000.0; winA[1] = 10000000.0; winA[2] = 0.0; winA[3] = 10000000.0;
}
else
{
if (magAD < magBD)
{
double[] diffAC = ArraySubtraction(A, OffPt);
double magAC = ArrayVectorMag(diffAC);
winA[0] = A[0]; winA[1] = A[1]; winA[2] = 0.0; winA[3] = magAC;
}
else
{
double[] diffBC = ArraySubtraction(B, OffPt);
double magBC = ArrayVectorMag(diffBC);
winA[0] = B[0]; winA[1] = B[1]; winA[2] = 0.0; winA[3] = magBC;
}
}
}
else
{
winA[0] = fx; winA[1] = fy; winA[2] = 0.0; winA[3] = DistMag;
}
return winA;
}
This technical solution allows us to solve about 90% of all the leader conditions. Not only that, it gives the “large numeral” puzzles kind of a sexy magnetized metal filing look. One person even said they liked the look of the uncompleted puzzle enough to consider just leaving it as is.
Even though this cleans up the leaders really nice, there are still some odd conditions that require some manual input. Also, I included a few conditionals to keep remote tags with the standard default string location. Also, “suburban” tags are rotated on the optimized angle, but not given a leader line. Lastly, the length of the leader line is inversely proportionate to the density of the point population in that locale. Naturally, there are CATIA coding that needed to be completed to reorient text so that it always faces the right directions (no mirror-text, and no up-side-down texts).
Regardless, it was a fun exercise, and we are trying to optimize this even further. Future enhancements will include stochastic simulated annealing to further optimize the orientation even more. Also, adding n-dimensional optimization to find the absolutely closest angle. Onward!

![[0001D] Automated Mega-Dots Tag and Leader Optimization](https://www.nickpisca.com/sherpa/wp-content/uploads/2015/09/20151112_XMLCTDImporter13.jpg)



![[Video] Figuring out an STL Export/Import Workflow from Maya to Sintratec Central](https://www.nickpisca.com/sherpa/wp-content/uploads/2019/05/20190506_bypasstitle-440x264.jpg)
Recent Comments