Here’s the problem: Given any three non-collinear coordinates in three-dimensions, find the circumcenter xyz coordinates in only simple arithmetic or parametric notation.
A collaboration with Clare Hemenway and Paul Martin.
It’s been a while since I posted to the blog, but it’s been a busy couple years. I have been doing a lot of interoperability projects, and they are fun tasks.
While working on a cylindrical concrete column structural interoperability project between different CAD applications, I ran into a unique mathematical situation. Sometimes when extracting the data from a cylindrical concrete column, you get the center point of the ends of the column. That makes the axis of the cylinder. However, sometimes you get three XYZ points on the perimeter of the circular ends of the concrete cylinder. I have to take those three points, draw a circle, then extract the center point using the CATIA HybridShapeCenter object, then delete the temporary circle. That is crazy expensive and slows the application to a much undesirable speed.
I knew there was a mathematical way to use 3 XYZ points and get the circumcenter, so I started to do the arithmetic. At first, we assumed all columns were perfectly vertical, so the circle was parallel to the XY Plane. After some simple y=mx+b intersection math, we came up with this subroutine (written in C#.net):
static double[] GetCircValues2(Vector3D A, Vector3D B, Vector3D C)
{
double[] circarr = { 0.0, 0.0, 0.0, 0.0, 0.0, 0.0 };
double Mac = (-(A.X - C.X) / (A.Y - C.Y));
double Mbc = (-(C.X - B.X) / (C.Y - B.Y));
double XV = ((A.Y / -2.0) + (Mac * ((A.X + C.X) / 2.0)) + (B.Y / 2.0) - (Mbc * ((B.X + C.X) / 2.0))) / (Mac - Mbc);
double YV = (Mac * XV) + ((A.Y + C.Y) / 2.0) - (Mac * ((A.X + C.X) / 2.0));
double ZV = A.Z;
Vector3D CenVec = new Vector3D(XV, YV, ZV);
Vector3D RadVec = A - CenVec;
double R = RadVec.Length;
circarr[0] = XV; circarr[1] = YV; circarr[2] = ZV; circarr[3] = R;
return circarr;
}
Well, that worked great until I encountered a sloped column, which occurs a lot on contemporary architectural and structural projects nowadays. Also, it required the vector math library, which I didn’t want to load. I googled to see if there was an example of three-dimensional circumcenter determination on the net, but unfortunately, there wasn’t much. Remembering some simple geometric rules like any bisector of an arc chord always crosses thru the center of a circle, and any two non-collinear chord bisectors always intersect at the center, and the cross product of the cords in the plane of the three points would give me the equation of the lines required in this exercise, I felt ready to tackle this task. I started to do the math, remembering my old linear algebra matrices and whatnot, but realized it had been about 15 years, so I was rusty. Not only did I want to figure out how to solve this, but I wanted it to be solvable in simple algebra, so there was no need for vector or complex math libraries to be referenced in this application.
That’s how I put in a “blast from the past” email to two very influential professors of mine back from UW-MC, Clare Hemenway and Paul Martin.
I explained the problem (Given any three non-collinear coordinates in three-dimensions, find the circumcenter xyz coordinates in only simple arithmetic or parametric notation. ) and asked if they knew of an old dusty book that might have the solution. Not only did they accept the challenge, but Paul promptly replied with a clearly-written proof and the output equations.
The equations are extremely long and rather than rewriting the steps here, I’ve pasted a screencapture into this post:
His math was air-tight. Now all I had to do was convert that to C#.net, or whatever language I felt like using. However, like all programming, I got tripped up on one character (a cubed instead of a squared) and was getting the wrong y-coordinate every time I executed the subroutine. It took me a day of letter by letter checking to find the bug, but now it works seamlessly.
Here’s the C#.net 3D GetCenter code.
static double[] GetCen(double r1o, double r2o, double r3o, double q1o, double q2o, double q3o, double p1o, double p2o, double p3o)
{
double r1 = r1o - p1o;
double r2 = r2o - p2o;
double r3 = r3o - p3o;
double q1 = q1o - p1o;
double q2 = q2o - p2o;
double q3 = q3o - p3o;
double t1 = r2 * q1 * Math.Pow(r3, 2.0) * q2; //NOTE: the negative is NOT included
double t2 = q1 * Math.Pow(r3, 2.0) * Math.Pow(q2, 2.0);
double t3 = r3 * q3 * r1 * Math.Pow(q2, 2.0);
double t4 = r3 * q3 * r1 * Math.Pow(q1, 2.0);
double t5 = r3 * q3 * Math.Pow(r1, 2.0) * q1;
double t6 = r3 * Math.Pow(r2, 2.0) * q3 * q1;
double t7 = Math.Pow(q3, 2.0) * r1 * Math.Pow(r3, 2.0);
double t8 = q1 * Math.Pow(r2, 3.0) * q2;
double t9 = q1 * Math.Pow(r2, 2.0) * Math.Pow(q2, 2.0);
double t10 = q1 * Math.Pow(r2, 2.0) * Math.Pow(q3, 2.0);
double t11 = r2 * Math.Pow(q1, 2.0) * r1 * q2;
double t12 = r2 * q1 * Math.Pow(r1, 2.0) * q2;
double t13 = q1 * Math.Pow(r3, 2.0) * Math.Pow(q3, 2.0);
double t14 = Math.Pow(r2, 2.0) * Math.Pow(q1, 3.0);
double t15 = Math.Pow(q1, 3.0) * Math.Pow(r3, 2.0);
double t16 = r3 * Math.Pow(q3, 3.0) * r1;
double t17 = Math.Pow(r1, 3.0) * Math.Pow(q3, 2.0);
double t18 = q3 * q1 * Math.Pow(r3, 3.0);
double t19 = Math.Pow(q2, 3.0) * r1 * r2;
double t20 = Math.Pow(q3, 2.0) * r1 * r2 * q2;
double t21 = r1 * Math.Pow(r2, 2.0) * Math.Pow(q3, 2.0);
double t22 = Math.Pow(r3, 2.0) * r1 * Math.Pow(q2, 2.0);
double t23 = Math.Pow(q2, 2.0) * r1 * Math.Pow(r2, 2.0);
double t24 = Math.Pow(r1, 3.0) * Math.Pow(q2, 2.0);
double numx = (-1 * t1) + t2 - t3 - t4 - t5 - t6 + t7 - t8 + t9 + t10 - t11 - t12 + t13 + t14 + t15 - t16 + t17 - t18 - t19 - t20 + t21 + t22 + t23 + t24;
double s1 = r2 * r1 * Math.Pow(q1, 3.0);
double s2 = Math.Pow(q1, 2.0) * Math.Pow(r2, 3.0);
double s3 = Math.Pow(q1, 2.0) * r2 * Math.Pow(r1, 2.0);
double s4 = Math.Pow(q1, 2.0) * r2 * q3 * r3;
double s5 = Math.Pow(q1, 2.0) * r2 * Math.Pow(r3, 2.0);
double s6 = Math.Pow(q1, 2.0) * Math.Pow(r3, 2.0) * q2;
double s7 = Math.Pow(q1, 2.0) * Math.Pow(r1, 2.0) * q2;
double s8 = q1 * Math.Pow(r2, 2.0) * q2 * r1;
double s9 = q1 * r2 * Math.Pow(q2, 2.0) * r1;
double s10 = q1 * r2 * Math.Pow(q3, 2.0) * r1;
double s11 = q1 * Math.Pow(r1, 3.0) * q2;
double s12 = q1 * Math.Pow(r3, 2.0) * r1 * q2;
double s13 = Math.Pow(q3, 2.0) * Math.Pow(r2, 3.0);
double s14 = r3 * q3 * q2 * Math.Pow(r2, 2.0);
double s15 = Math.Pow(r3, 2.0) * r2 * Math.Pow(q3, 2.0);
double s16 = r2 * Math.Pow(q3, 2.0) * Math.Pow(r1, 2.0);
double s17 = r2 * r3 * q3 * Math.Pow(q2, 2.0);
double s18 = r2 * r3 * Math.Pow(q3, 3.0);
double s19 = Math.Pow(q2, 3.0) * Math.Pow(r1, 2.0);
double s20 = q3 * Math.Pow(r3, 3.0) * q2;
double s21 = r3 * q3 * Math.Pow(r1, 2.0) * q2;
double s22 = Math.Pow(q3, 2.0) * Math.Pow(r1, 2.0) * q2;
double s23 = Math.Pow(r3, 2.0) * Math.Pow(q2, 3.0);
double s24 = Math.Pow(r3, 2.0) * q2 * Math.Pow(q3, 2.0);
double numy = s1 - s2 - s3 + s4 - s5 - s6 - s7 + s8 + s9 + s10 + s11 + s12 - s13 + s14 - s15 - s16 + s17 + s18 - s19 + s20 + s21 - s22 - s23 - s24;
double v1 = q3 * Math.Pow(r1, 2.0) * Math.Pow(q2, 2.0); //negative not put on this variable
double v2 = q3 * Math.Pow(r1, 2.0) * Math.Pow(q1, 2.0);
double v3 = Math.Pow(r3, 3.0) * Math.Pow(q2, 2.0);
double v4 = Math.Pow(r2, 2.0) * Math.Pow(q3, 3.0);
double v5 = Math.Pow(q1, 2.0) * Math.Pow(r3, 3.0);
double v6 = q3 * Math.Pow(r1, 3.0) * q1;
double v7 = Math.Pow(q1, 2.0) * r3 * Math.Pow(r1, 2.0);
double v8 = r3 * Math.Pow(q2, 2.0) * Math.Pow(r1, 2.0);
double v9 = Math.Pow(q1, 3.0) * r3 * r1;
double v10 = r3 * q2 * r2 * Math.Pow(q3, 2.0);
double v11 = r2 * q3 * Math.Pow(r3, 2.0) * q2;
double v12 = q1 * r3 * r1 * Math.Pow(q3, 2.0);
double v13 = q3 * r1 * q1 * Math.Pow(r3, 2.0);
double v14 = Math.Pow(q3, 3.0) * Math.Pow(r1, 2.0);
double v15 = r3 * Math.Pow(q2, 3.0) * r2;
double v16 = Math.Pow(r2, 2.0) * q3 * q1 * r1;
double v17 = Math.Pow(r2, 2.0) * q3 * Math.Pow(q1, 2.0);
double v18 = Math.Pow(r2, 2.0) * q3 * Math.Pow(q2, 2.0);
double v19 = Math.Pow(q1, 2.0) * r3 * Math.Pow(r2, 2.0);
double v20 = q1 * r3 * r1 * Math.Pow(q2, 2.0);
double v21 = r3 * Math.Pow(q2, 2.0) * Math.Pow(r2, 2.0);
double v22 = r2 * q3 * Math.Pow(r1, 2.0) * q2;
double v23 = Math.Pow(r2, 3.0) * q3 * q2;
double v24 = r3 * q2 * r2 * Math.Pow(q1, 2.0);
double numz = (-1 * v1) - v2 - v3 - v4 - v5 + v6 - v7 - v8 + v9 + v10 + v11 + v12 + v13 - v14 + v15 + v16 - v17 - v18 - v19 + v20 - v21 + v22 + v23 + v24;
double n1 = Math.Pow(q2, 2.0) * Math.Pow(r1, 2.0);
double n2 = Math.Pow(q3, 2.0) * Math.Pow(r1, 2.0);
double n3 = Math.Pow(r2, 2.0) * Math.Pow(q3, 2.0);
double n4 = Math.Pow(q1, 2.0) * Math.Pow(r3, 2.0);
double n5 = Math.Pow(r3, 2.0) * Math.Pow(q2, 2.0);
double n6 = Math.Pow(q1, 2.0) * Math.Pow(r2, 2.0);
double n7 = 2 * r3 * q2 * r2 * q3;
double n8 = 2 * q3 * r1 * q1 * r3;
double n9 = 2 * q1 * r2 * r1 * q2;
double den = n1 + n2 + n3 + n4 + n5 + n6 - n7 - n8 - n9;
if (den != 0.0)
{
double x = (0.5 * (numx / den)) + p1o;
double y = ((-0.5) * (numy / den)) + p2o;
double z = ((-0.5) * (numz / den)) + p3o;
double[] xyz = { x, y, z };
return xyz;
}
return null;
}
//Example:
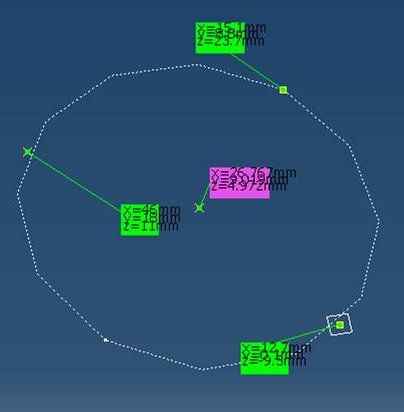
double[] xyz = GetCen(15.1, 8.8, 23.7, 12.7, 0.1, -9.5, 46.0, 18.0, 11.0);
//returns: xyz = (26.767, 9.019, 4.972)
Well, I just wanted to post the fruits of this great collaboration, so that other coders can utilize these equations. Since it only uses basic math (you could even eliminate the Math.Pow methods with just multiplication if necessary), it’s easily convertible into VB, Python, etc, etc. I see so many benefits to having a circumcenter calculation in simple math for game development, complex CAD systems, and so on.
Thanks again to Clare Hemenway and Paul Martin for their help.



![[0001D Video] Timelapse of “Randomized Node” Polyline Drawing](https://www.nickpisca.com/sherpa/wp-content/uploads/2015/03/20150302_MTloting2sfw.jpg)

Learned a bunch. Quite simple to fully grasp. Nice one for sharing with us 🙂